SPIN Centre for Chemical Engineering
FR
Rechercher
Fermer
Menu

SPIN Centre for Chemical Engineering

Home | Expertise | Image analysis

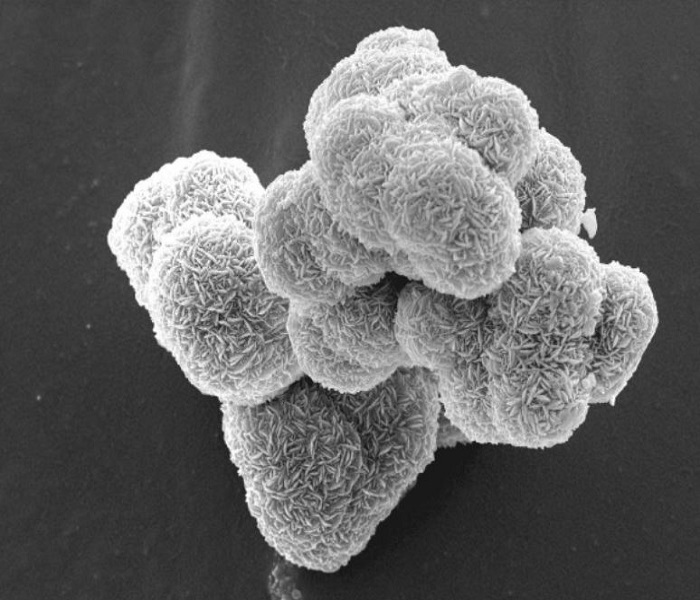
Image analysis

Images are useful for characterizing materials or processes, especially when dealing with dispersed media such as grains, bubbles, droplets or pores.

Zinc sulphide agregate Human corneal endothelium Ammonium oxalate crystals Two-phase flow

 
In our group, we develop methods and tools to process, analyze and model images of dispersed media. The image processing simplifies the raw image to identify the objects of interest by filtering, thresholding, … The image analysis performs morphological measurements on these objects (shape, size, dispersion, …). The geometrical modeling aims at generating synthesis images (numerical twins) that share the same statistical properties as the original ones and, by comparison and iteration, extract robust information on the shape and size for instance.

Image processing

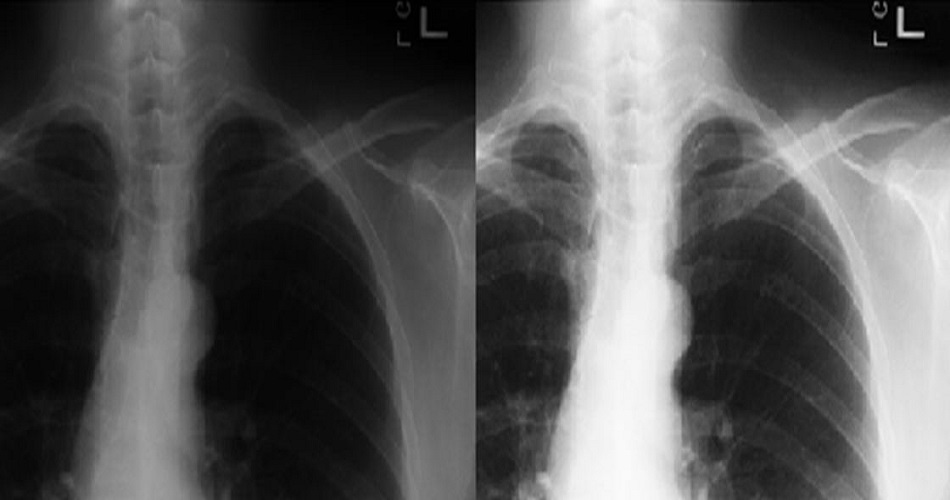
Logarithmic image processing (LIP)

The logarithmic image processing approach is a mathematical framework introduced in the 80’s, based on abstract linear mathematics. It gives a number of algebraic and functional operations applicable to intensity images.

General adaptive neighborhood image processing

The general adaptive neighborhood image processing is a mathematical framework developed for grayscale images. An image is represented by an ensemble of local neighborhoods defined for each pixel. These neighborhoods are then used as adaptive operational windows for local transformations (morphological filters) and for local analysis (local descriptors).

Image analysis

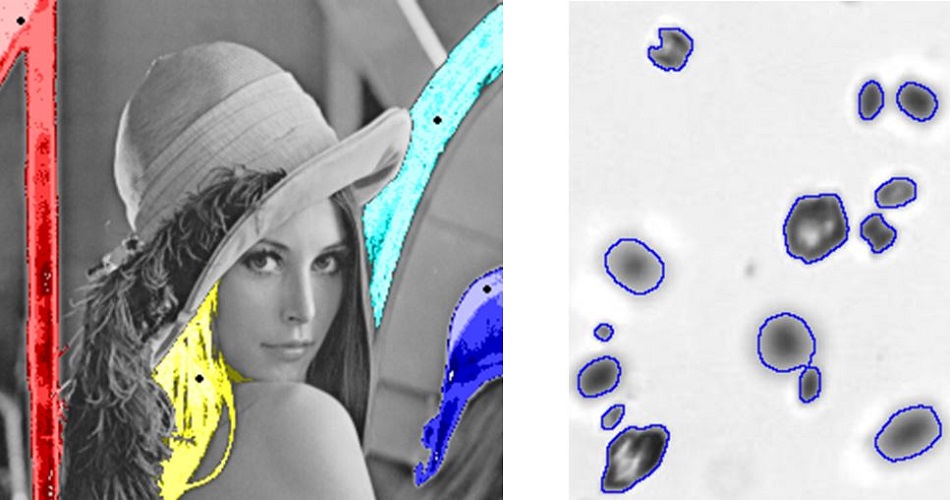
Shape analysis

The goal is to give a quantitative morphological description of the patterns of interest. Shape diagrams are used to represent a shape by a point in a unit square, which allows for shape discrimination. For complex objects as aggregates, specific descriptors are used.

Image modeling

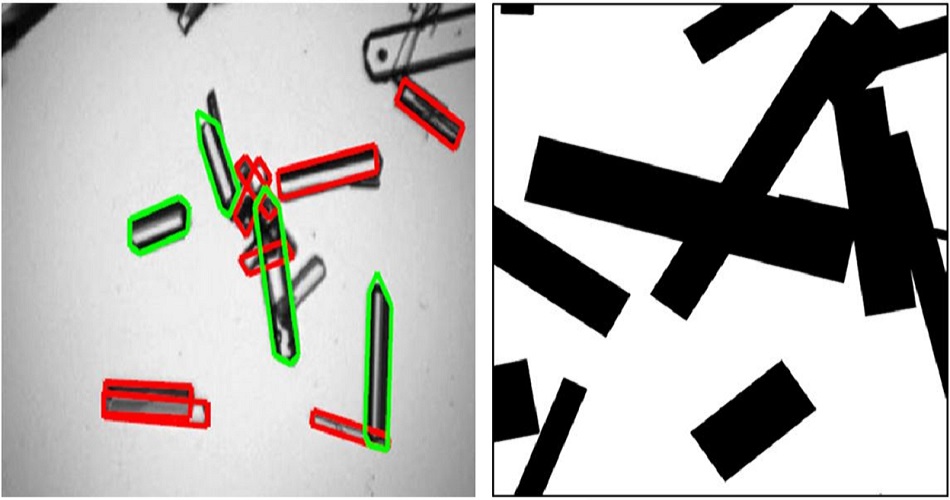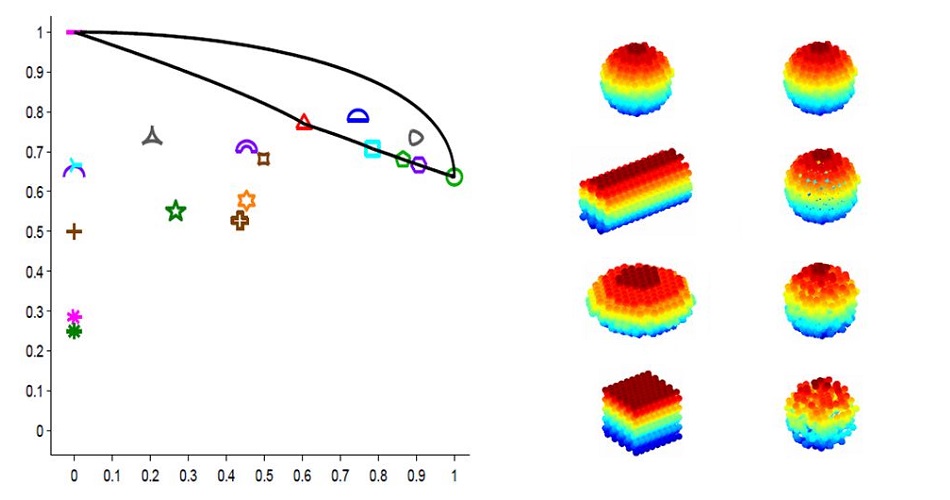
Stochastic modeling of images and shapes

In order to characterize the geometry of complex spatial structures, we use stochastic processes to generate synthesis images, representative of real ones. For instance, boolean models (union of random basic geometrical ensembles) can be used to indirectly characterize complex structures.

Mosaic simulation and modeling

Voronoi diagrams are classically used to model mosaic patterns, such as grains, foam cells, pores or biological cells. It can be combined with a random fields study to determine the seeds/centers and the distances to generate a 2D or 3D spatial pavement.

Group members